Lux.jl
Fitting a Polynomial using MLP
In this tutorial we will fit a MultiLayer Perceptron (MLP) on data generated from a polynomial.
Package Imports
using Lux
using LuxAMDGPU,
LuxCUDA, Optimisers, Random, Statistics, Zygote, CairoMakie, MakiePublication
Activating project at `/var/lib/buildkite-agent/builds/gpuci-11/julialang/lux-dot-jl/examples`
Dataset
Generate 128 datapoints from the polynomial $y = x^2 - 2x$.
function generate_data(rng::AbstractRNG)
x = reshape(collect(range(-2.0f0, 2.0f0, 128)), (1, 128))
y = evalpoly.(x, ((0, -2, 1),)) .+ randn(rng, (1, 128)) .* 0.1f0
return (x, y)
end
generate_data (generic function with 1 method)
Initialize the random number generator and fetch the dataset.
rng = MersenneTwister()
Random.seed!(rng, 12345)
(x, y) = generate_data(rng)
(Float32[-2.0 -1.968504 … 1.968504 2.0], [8.11723579535073 7.8972862806322315 … -0.21213293699653427 0.049985105882301])
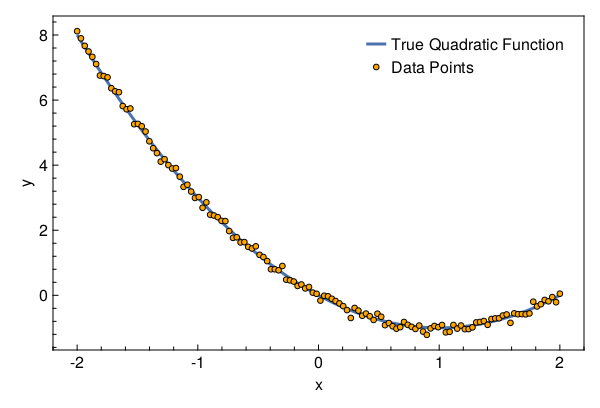
Let’s visualize the dataset
with_theme(theme_web()) do
fig = Figure()
ax = CairoMakie.Axis(fig[1, 1]; xlabel="x", ylabel="y")
l = lines!(ax, x[1, :], x -> evalpoly(x, (0, -2, 1)); linewidth=3)
s = scatter!(ax, x[1, :], y[1, :]; markersize=8, color=:orange,
strokecolor=:black, strokewidth=1)
axislegend(ax, [l, s], ["True Quadratic Function", "Data Points"])
return fig
end
Neural Network
For this problem, you should not be using a neural network. But let’s still do that!
model = Chain(Dense(1 => 16, relu), Dense(16 => 1))
Chain(
layer_1 = Dense(1 => 16, relu), # 32 parameters
layer_2 = Dense(16 => 1), # 17 parameters
) # Total: 49 parameters,
# plus 0 states.
Optimizer
We will use Adam from Optimisers.jl
opt = Adam(0.03f0)
Optimisers.Adam{Float32}(0.03f0, (0.9f0, 0.999f0), 1.1920929f-7)
Loss Function
We will use the Lux.Training API so we need to ensure that our loss function takes 4 inputs – model, parameters, states and data. The function must return 3 values – loss, updated_state, and any computed statistics.
function loss_function(model, ps, st, data)
y_pred, st = Lux.apply(model, data[1], ps, st)
mse_loss = mean(abs2, y_pred .- data[2])
return mse_loss, st, ()
end
loss_function (generic function with 1 method)
Training
First we will create a Lux.Experimental.TrainState which is essentially a convenience wrapper over parameters, states and optimizer states.
tstate = Lux.Training.TrainState(rng, model, opt)
Lux.Experimental.TrainState{Chain{NamedTuple{(:layer_1, :layer_2), Tuple{Dense{true, typeof(relu), typeof(glorot_uniform), typeof(zeros32)}, Dense{true, typeof(identity), typeof(glorot_uniform), typeof(zeros32)}}}, Nothing}, NamedTuple{(:layer_1, :layer_2), Tuple{NamedTuple{(:weight, :bias), Tuple{CuArray{Float32, 2, CUDA.Mem.DeviceBuffer}, CuArray{Float32, 2, CUDA.Mem.DeviceBuffer}}}, NamedTuple{(:weight, :bias), Tuple{CuArray{Float32, 2, CUDA.Mem.DeviceBuffer}, CuArray{Float32, 2, CUDA.Mem.DeviceBuffer}}}}}, NamedTuple{(:layer_1, :layer_2), Tuple{NamedTuple{(), Tuple{}}, NamedTuple{(), Tuple{}}}}, NamedTuple{(:layer_1, :layer_2), Tuple{NamedTuple{(:weight, :bias), Tuple{Optimisers.Leaf{Optimisers.Adam{Float32}, Tuple{CuArray{Float32, 2, CUDA.Mem.DeviceBuffer}, CuArray{Float32, 2, CUDA.Mem.DeviceBuffer}, Tuple{Float32, Float32}}}, Optimisers.Leaf{Optimisers.Adam{Float32}, Tuple{CuArray{Float32, 2, CUDA.Mem.DeviceBuffer}, CuArray{Float32, 2, CUDA.Mem.DeviceBuffer}, Tuple{Float32, Float32}}}}}, NamedTuple{(:weight, :bias), Tuple{Optimisers.Leaf{Optimisers.Adam{Float32}, Tuple{CuArray{Float32, 2, CUDA.Mem.DeviceBuffer}, CuArray{Float32, 2, CUDA.Mem.DeviceBuffer}, Tuple{Float32, Float32}}}, Optimisers.Leaf{Optimisers.Adam{Float32}, Tuple{CuArray{Float32, 2, CUDA.Mem.DeviceBuffer}, CuArray{Float32, 2, CUDA.Mem.DeviceBuffer}, Tuple{Float32, Float32}}}}}}}}(Chain(), (layer_1 = (weight = Float32[0.36222202; 0.23371002; … ; 0.5260752; -0.07562564;;], bias = Float32[0.0; 0.0; … ; 0.0; 0.0;;]), layer_2 = (weight = Float32[-0.14330137 -0.39328107 … -0.34761065 -0.05758927], bias = Float32[0.0;;])), (layer_1 = NamedTuple(), layer_2 = NamedTuple()), (layer_1 = (weight = Leaf(Adam{Float32}(0.03, (0.9, 0.999), 1.19209f-7), (Float32[0.0; 0.0; … ; 0.0; 0.0;;], Float32[0.0; 0.0; … ; 0.0; 0.0;;], (0.9, 0.999))), bias = Leaf(Adam{Float32}(0.03, (0.9, 0.999), 1.19209f-7), (Float32[0.0; 0.0; … ; 0.0; 0.0;;], Float32[0.0; 0.0; … ; 0.0; 0.0;;], (0.9, 0.999)))), layer_2 = (weight = Leaf(Adam{Float32}(0.03, (0.9, 0.999), 1.19209f-7), (Float32[0.0 0.0 … 0.0 0.0], Float32[0.0 0.0 … 0.0 0.0], (0.9, 0.999))), bias = Leaf(Adam{Float32}(0.03, (0.9, 0.999), 1.19209f-7), (Float32[0.0;;], Float32[0.0;;], (0.9, 0.999))))), 0)
Now we will use Zygote for our AD requirements.
vjp_rule = Lux.Training.AutoZygote()
ADTypes.AutoZygote()
Finally the training loop.
function main(tstate::Lux.Experimental.TrainState, vjp, data, epochs)
data = data .|> gpu_device()
for epoch in 1:epochs
grads, loss, stats, tstate = Lux.Training.compute_gradients(vjp,
loss_function, data, tstate)
@info epoch=epoch loss=loss
tstate = Lux.Training.apply_gradients(tstate, grads)
end
return tstate
end
dev_cpu = cpu_device()
dev_gpu = gpu_device()
tstate = main(tstate, vjp_rule, (x, y), 250)
y_pred = dev_cpu(Lux.apply(tstate.model, dev_gpu(x), tstate.parameters, tstate.states)[1])
1×128 Matrix{Float32}:
7.93183 7.76661 7.60138 7.43616 … -0.305276 -0.280904 -0.256532
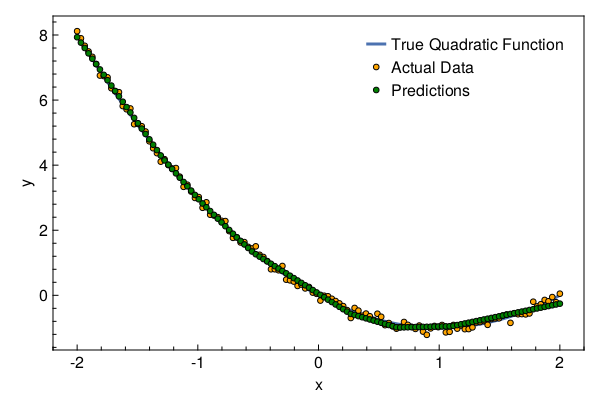
Let’s plot the results
with_theme(theme_web()) do
fig = Figure()
ax = CairoMakie.Axis(fig[1, 1]; xlabel="x", ylabel="y")
l = lines!(ax, x[1, :], x -> evalpoly(x, (0, -2, 1)); linewidth=3)
s1 = scatter!(ax, x[1, :], y[1, :]; markersize=8, color=:orange,
strokecolor=:black, strokewidth=1)
s2 = scatter!(ax, x[1, :], y_pred[1, :]; markersize=8, color=:green,
strokecolor=:black, strokewidth=1)
axislegend(ax, [l, s1, s2], ["True Quadratic Function", "Actual Data", "Predictions"])
return fig
end
This page was generated using Literate.jl.