Bayesian Neural Network
We borrow this tutorial from the official Turing Docs. We will show how the explicit parameterization of Lux enables first-class composability with packages which expect flattened out parameter vectors.
Note: The tutorial in the official Turing docs is now using Lux instead of Flux.
We will use Turing.jl with Lux.jl to implement implementing a classification algorithm. Lets start by importing the relevant libraries.
# Import libraries
using Lux, Turing, CairoMakie, Random, Tracker, Functors, LinearAlgebra
# Sampling progress
Turing.setprogress!(true);[ Info: [Turing]: progress logging is enabled globally
[ Info: [AdvancedVI]: global PROGRESS is set as trueGenerating data
Our goal here is to use a Bayesian neural network to classify points in an artificial dataset. The code below generates data points arranged in a box-like pattern and displays a graph of the dataset we'll be working with.
# Number of points to generate
N = 80
M = round(Int, N / 4)
rng = Random.default_rng()
Random.seed!(rng, 1234)
# Generate artificial data
x1s = rand(rng, Float32, M) * 4.5f0;
x2s = rand(rng, Float32, M) * 4.5f0;
xt1s = Array([[x1s[i] + 0.5f0; x2s[i] + 0.5f0] for i in 1:M])
x1s = rand(rng, Float32, M) * 4.5f0;
x2s = rand(rng, Float32, M) * 4.5f0;
append!(xt1s, Array([[x1s[i] - 5.0f0; x2s[i] - 5.0f0] for i in 1:M]))
x1s = rand(rng, Float32, M) * 4.5f0;
x2s = rand(rng, Float32, M) * 4.5f0;
xt0s = Array([[x1s[i] + 0.5f0; x2s[i] - 5.0f0] for i in 1:M])
x1s = rand(rng, Float32, M) * 4.5f0;
x2s = rand(rng, Float32, M) * 4.5f0;
append!(xt0s, Array([[x1s[i] - 5.0f0; x2s[i] + 0.5f0] for i in 1:M]))
# Store all the data for later
xs = [xt1s; xt0s]
ts = [ones(2 * M); zeros(2 * M)]
# Plot data points
function plot_data()
x1 = first.(xt1s)
y1 = last.(xt1s)
x2 = first.(xt0s)
y2 = last.(xt0s)
fig = Figure()
ax = CairoMakie.Axis(fig[1, 1]; xlabel="x", ylabel="y")
scatter!(ax, x1, y1; markersize=16, color=:red, strokecolor=:black, strokewidth=2)
scatter!(ax, x2, y2; markersize=16, color=:blue, strokecolor=:black, strokewidth=2)
return fig
end
plot_data()Building the Neural Network
The next step is to define a feedforward neural network where we express our parameters as distributions, and not single points as with traditional neural networks. For this we will use Dense to define liner layers and compose them via Chain, both are neural network primitives from Lux. The network nn we will create will have two hidden layers with tanh activations and one output layer with sigmoid activation, as shown below.
The nn is an instance that acts as a function and can take data, parameters and current state as inputs and output predictions. We will define distributions on the neural network parameters.
# Construct a neural network using Lux
nn = Chain(Dense(2 => 3, tanh), Dense(3 => 2, tanh), Dense(2 => 1, sigmoid))
# Initialize the model weights and state
ps, st = Lux.setup(rng, nn)
Lux.parameterlength(nn) # number of parameters in NN20The probabilistic model specification below creates a parameters variable, which has IID normal variables. The parameters represents all parameters of our neural net (weights and biases).
# Create a regularization term and a Gaussian prior variance term.
alpha = 0.09
sig = sqrt(1.0 / alpha)3.3333333333333335Construct named tuple from a sampled parameter vector. We could also use ComponentArrays here and simply broadcast to avoid doing this. But let's do it this way to avoid dependencies.
function vector_to_parameters(ps_new::AbstractVector, ps::NamedTuple)
@assert length(ps_new) == Lux.parameterlength(ps)
i = 1
function get_ps(x)
z = reshape(view(ps_new, i:(i + length(x) - 1)), size(x))
i += length(x)
return z
end
return fmap(get_ps, ps)
endvector_to_parameters (generic function with 1 method)To interface with external libraries it is often desirable to use the StatefulLuxLayer to automatically handle the neural network states.
const model = StatefulLuxLayer{true}(nn, nothing, st)
# Specify the probabilistic model.
@model function bayes_nn(xs, ts)
# Sample the parameters
nparameters = Lux.parameterlength(nn)
parameters ~ MvNormal(zeros(nparameters), Diagonal(abs2.(sig .* ones(nparameters))))
# Forward NN to make predictions
preds = Lux.apply(model, xs, vector_to_parameters(parameters, ps))
# Observe each prediction.
for i in eachindex(ts)
ts[i] ~ Bernoulli(preds[i])
end
endbayes_nn (generic function with 2 methods)Inference can now be performed by calling sample. We use the HMC sampler here.
# Perform inference.
N = 5000
ch = sample(bayes_nn(reduce(hcat, xs), ts), HMC(0.05, 4; adtype=AutoTracker()), N)Chains MCMC chain (5000×30×1 Array{Float64, 3}):
Iterations = 1:1:5000
Number of chains = 1
Samples per chain = 5000
Wall duration = 64.98 seconds
Compute duration = 64.98 seconds
parameters = parameters[1], parameters[2], parameters[3], parameters[4], parameters[5], parameters[6], parameters[7], parameters[8], parameters[9], parameters[10], parameters[11], parameters[12], parameters[13], parameters[14], parameters[15], parameters[16], parameters[17], parameters[18], parameters[19], parameters[20]
internals = lp, n_steps, is_accept, acceptance_rate, log_density, hamiltonian_energy, hamiltonian_energy_error, numerical_error, step_size, nom_step_size
Summary Statistics
parameters mean std mcse ess_bulk ess_tail rhat ess_per_sec
Symbol Float64 Float64 Float64 Float64 Float64 Float64 Float64
parameters[1] 2.0965 4.4644 1.3270 12.0887 23.0787 1.3335 0.1860
parameters[2] 0.0843 0.3952 0.0510 79.9413 35.2287 1.0240 1.2302
parameters[3] 4.9916 1.9230 0.4456 19.3935 81.5852 1.2170 0.2984
parameters[4] 0.3356 2.3096 0.6117 14.3653 24.1405 1.2067 0.2211
parameters[5] 5.0569 2.3192 0.6141 15.0672 34.9402 1.1058 0.2319
parameters[6] 0.7127 1.2191 0.2991 21.7200 21.7891 1.1550 0.3343
parameters[7] 1.7149 3.8638 1.1143 12.4420 21.7560 1.1439 0.1915
parameters[8] 0.3690 1.2835 0.2555 26.1914 29.6846 1.0246 0.4031
parameters[9] -0.4968 2.2271 0.6133 14.1406 24.5983 1.2648 0.2176
parameters[10] 0.0842 2.1828 0.5840 14.0865 21.8689 1.1832 0.2168
parameters[11] -1.0288 1.5663 0.3628 18.3294 27.7789 1.0536 0.2821
parameters[12] -4.1763 1.7426 0.3705 23.0782 28.1565 1.0633 0.3552
parameters[13] 3.1846 1.4791 0.3401 19.4472 53.5564 1.0444 0.2993
parameters[14] 2.7199 1.9547 0.5178 14.3490 46.8984 1.3048 0.2208
parameters[15] -2.0613 1.4937 0.3727 16.3035 39.2852 1.0885 0.2509
parameters[16] -2.9853 1.4059 0.2557 31.3669 31.3956 1.0012 0.4827
parameters[17] -2.4061 2.6897 0.7370 15.6752 20.0204 1.0733 0.2412
parameters[18] -5.3040 1.1943 0.1791 44.9414 68.7121 1.0867 0.6916
parameters[19] -5.1706 2.2709 0.5991 17.6788 18.3886 1.0540 0.2721
parameters[20] -5.1303 1.3008 0.2366 30.4880 60.9517 1.0163 0.4692
Quantiles
parameters 2.5% 25.0% 50.0% 75.0% 97.5%
Symbol Float64 Float64 Float64 Float64 Float64
parameters[1] -7.7024 0.5794 2.9500 5.0242 8.8277
parameters[2] -0.6189 -0.1406 0.0435 0.2877 1.0813
parameters[3] 1.2261 3.6852 4.9109 6.5386 8.2717
parameters[4] -3.9045 -0.9307 0.1458 1.1265 5.7834
parameters[5] 1.5809 3.2130 4.8534 6.4543 10.0149
parameters[6] -0.8100 -0.0584 0.3864 1.1121 4.4225
parameters[7] -5.8787 -0.8376 1.2050 4.7533 8.9694
parameters[8] -2.3155 -0.3960 0.2950 1.1550 2.9515
parameters[9] -5.8990 -1.7942 -0.1511 1.0876 2.9460
parameters[10] -4.7703 -1.0568 0.0534 1.4673 4.2833
parameters[11] -4.5806 -1.9640 -0.8771 0.0209 1.7384
parameters[12] -8.2243 -5.3092 -4.0546 -2.7977 -1.3694
parameters[13] 0.8904 2.0618 2.9913 4.0971 6.5956
parameters[14] -0.9166 1.5821 2.5812 3.9071 6.6712
parameters[15] -4.9708 -3.1310 -2.0122 -1.0256 0.7273
parameters[16] -6.2647 -3.8094 -2.8050 -1.8812 -0.8946
parameters[17] -6.2695 -3.8672 -2.6943 -1.7352 5.5834
parameters[18] -7.6970 -6.0973 -5.2714 -4.5053 -2.9747
parameters[19] -8.3524 -6.4017 -5.5673 -4.6134 2.1958
parameters[20] -7.6214 -5.9847 -5.1652 -4.2672 -2.6349Now we extract the parameter samples from the sampled chain as θ (this is of size 5000 x 20 where 5000 is the number of iterations and 20 is the number of parameters). We'll use these primarily to determine how good our model's classifier is.
# Extract all weight and bias parameters.
θ = MCMCChains.group(ch, :parameters).value;Prediction Visualization
# A helper to run the nn through data `x` using parameters `θ`
nn_forward(x, θ) = model(x, vector_to_parameters(θ, ps))
# Plot the data we have.
fig = plot_data()
# Find the index that provided the highest log posterior in the chain.
_, i = findmax(ch[:lp])
# Extract the max row value from i.
i = i.I[1]
# Plot the posterior distribution with a contour plot
x1_range = collect(range(-6; stop=6, length=25))
x2_range = collect(range(-6; stop=6, length=25))
Z = [nn_forward([x1, x2], θ[i, :])[1] for x1 in x1_range, x2 in x2_range]
contour!(x1_range, x2_range, Z; linewidth=3, colormap=:seaborn_bright)
figThe contour plot above shows that the MAP method is not too bad at classifying our data. Now we can visualize our predictions.
The nn_predict function takes the average predicted value from a network parameterized by weights drawn from the MCMC chain.
# Return the average predicted value across multiple weights.
nn_predict(x, θ, num) = mean([first(nn_forward(x, view(θ, i, :))) for i in 1:10:num])nn_predict (generic function with 1 method)Next, we use the nn_predict function to predict the value at a sample of points where the x1 and x2 coordinates range between -6 and 6. As we can see below, we still have a satisfactory fit to our data, and more importantly, we can also see where the neural network is uncertain about its predictions much easier–-those regions between cluster boundaries.
Plot the average prediction.
fig = plot_data()
n_end = 1500
x1_range = collect(range(-6; stop=6, length=25))
x2_range = collect(range(-6; stop=6, length=25))
Z = [nn_predict([x1, x2], θ, n_end)[1] for x1 in x1_range, x2 in x2_range]
contour!(x1_range, x2_range, Z; linewidth=3, colormap=:seaborn_bright)
figSuppose we are interested in how the predictive power of our Bayesian neural network evolved between samples. In that case, the following graph displays an animation of the contour plot generated from the network weights in samples 1 to 5,000.
fig = plot_data()
Z = [first(nn_forward([x1, x2], θ[1, :])) for x1 in x1_range, x2 in x2_range]
c = contour!(x1_range, x2_range, Z; linewidth=3, colormap=:seaborn_bright)
record(fig, "results.gif", 1:250:size(θ, 1)) do i
fig.current_axis[].title = "Iteration: $i"
Z = [first(nn_forward([x1, x2], θ[i, :])) for x1 in x1_range, x2 in x2_range]
c[3] = Z
return fig
end"results.gif"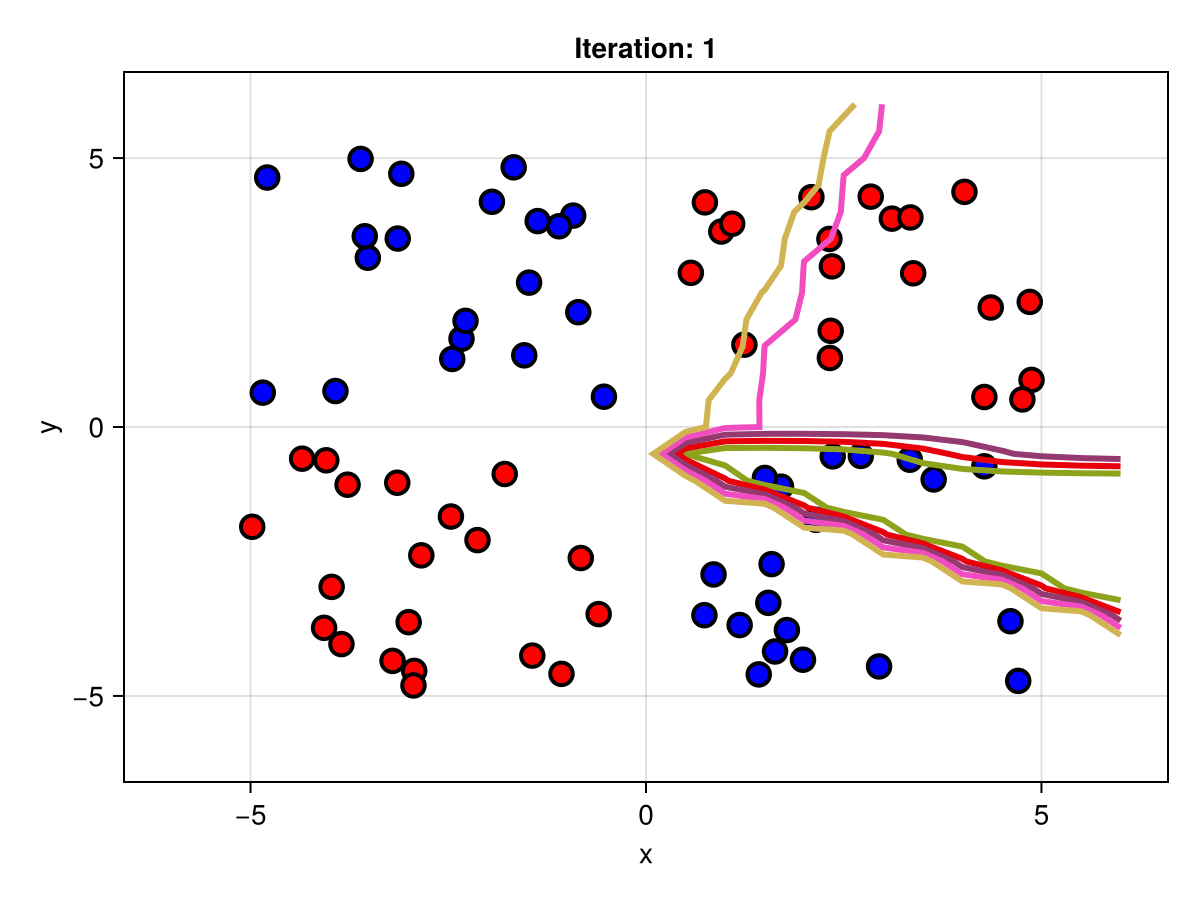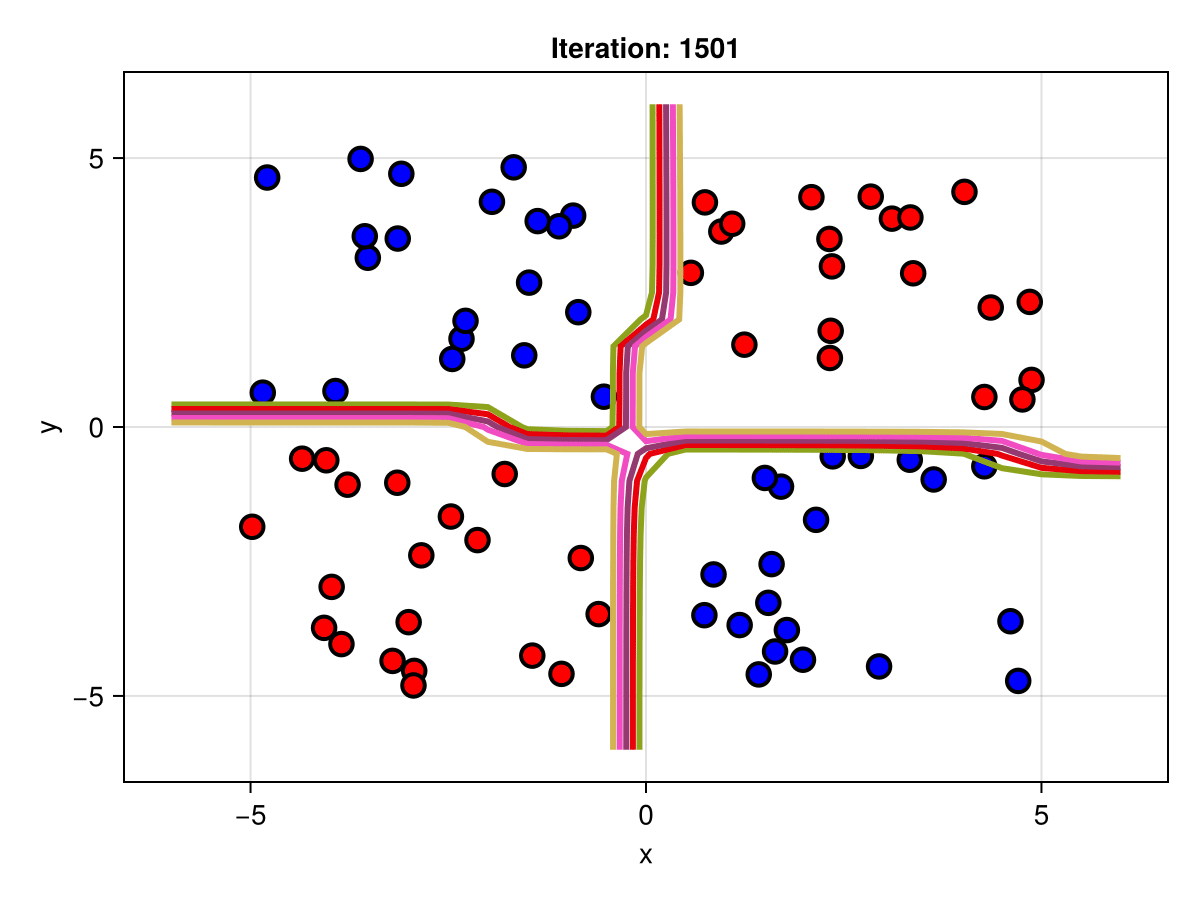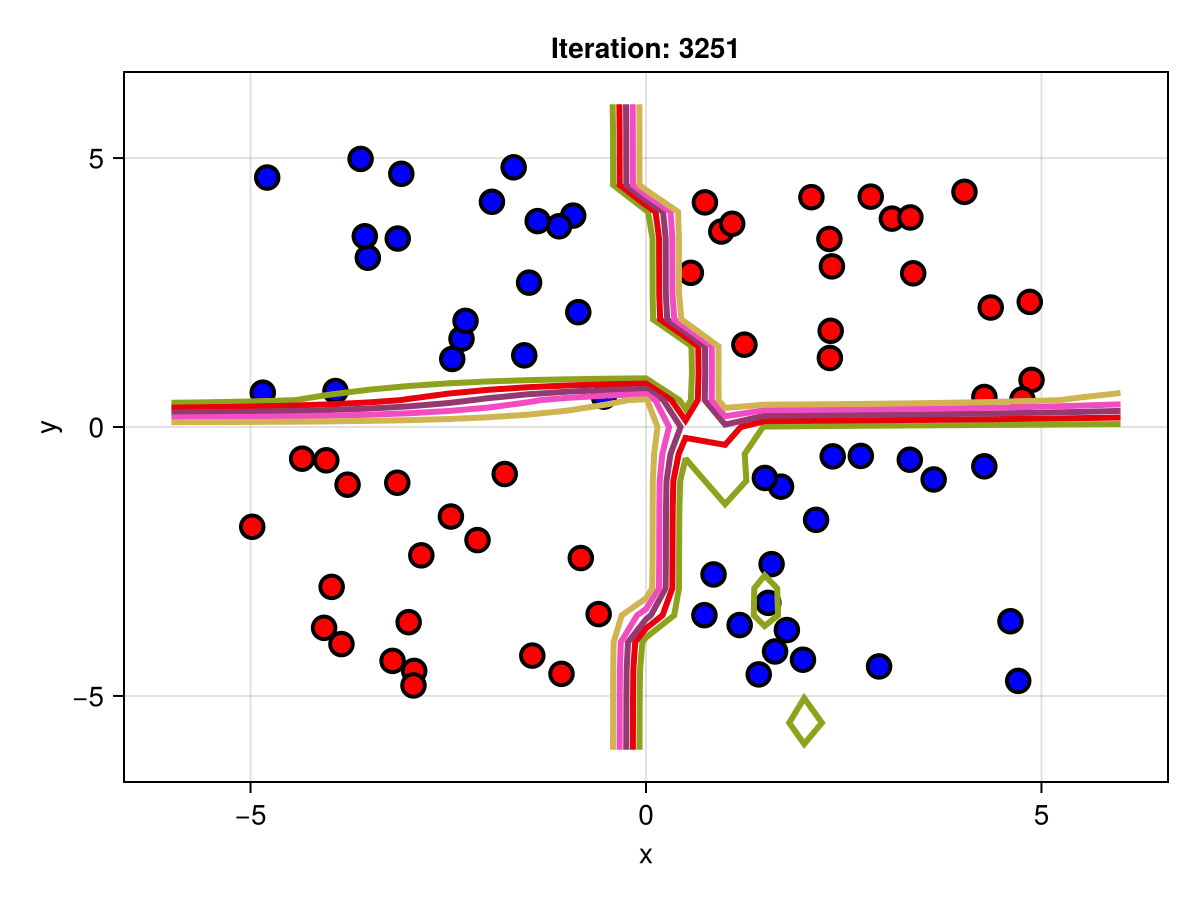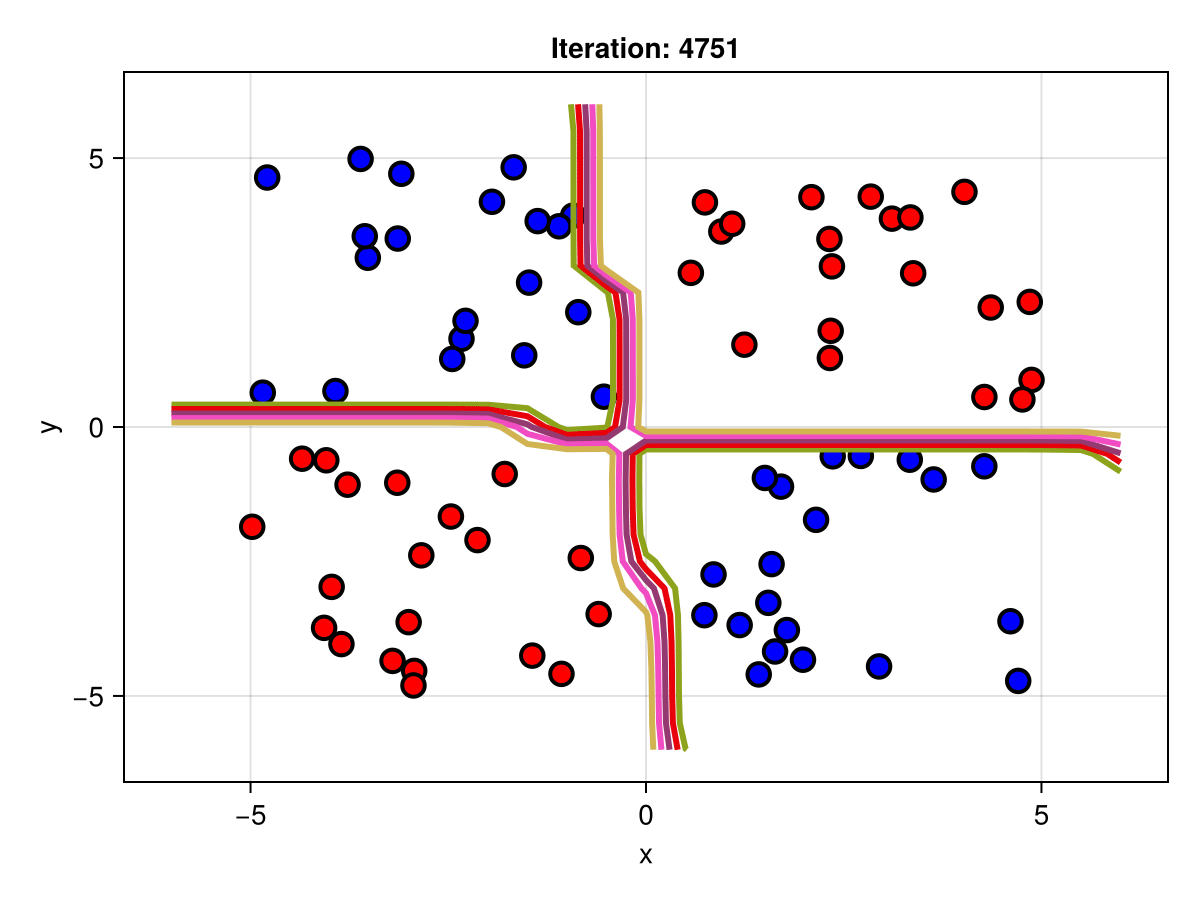
Appendix
using InteractiveUtils
InteractiveUtils.versioninfo()
if @isdefined(MLDataDevices)
if @isdefined(CUDA) && MLDataDevices.functional(CUDADevice)
println()
CUDA.versioninfo()
end
if @isdefined(AMDGPU) && MLDataDevices.functional(AMDGPUDevice)
println()
AMDGPU.versioninfo()
end
endJulia Version 1.10.5
Commit 6f3fdf7b362 (2024-08-27 14:19 UTC)
Build Info:
Official https://julialang.org/ release
Platform Info:
OS: Linux (x86_64-linux-gnu)
CPU: 128 × AMD EPYC 7502 32-Core Processor
WORD_SIZE: 64
LIBM: libopenlibm
LLVM: libLLVM-15.0.7 (ORCJIT, znver2)
Threads: 16 default, 0 interactive, 8 GC (on 16 virtual cores)
Environment:
JULIA_CPU_THREADS = 16
JULIA_DEPOT_PATH = /cache/julia-buildkite-plugin/depots/01872db4-8c79-43af-ab7d-12abac4f24f6
JULIA_PKG_SERVER =
JULIA_NUM_THREADS = 16
JULIA_CUDA_HARD_MEMORY_LIMIT = 100%
JULIA_PKG_PRECOMPILE_AUTO = 0
JULIA_DEBUG = LiterateThis page was generated using Literate.jl.