Not Run on CI

This tutorial is not run on CI to reduce the computational burden. If you encounter any issues, please open an issue on the Lux.jl repository.

Normalizing Flows for Density Estimation

This tutorial demonstrates how to use Lux to train a RealNVP. This is based on the RealNVP implementation in MLX.

using Lux,
    Reactant,
    Random,
    Statistics,
    Enzyme,
    MLUtils,
    ConcreteStructs,
    Printf,
    Optimisers,
    CairoMakie

const xdev = reactant_device(; force=true)
const cdev = cpu_device()

Define & Load the Moons Dataset

We define a function to generate data from the moons dataset. We use the code here from this tutorial.

function make_moons(
    rng::AbstractRNG,
    ::Type{T},
    n_samples::Int=100;
    noise::Union{Nothing,AbstractFloat}=nothing,
) where {T}
    n_moons = n_samples ÷ 2
    t_min, t_max = T(0), T(π)
    t_inner = rand(rng, T, n_moons) * (t_max - t_min) .+ t_min
    t_outer = rand(rng, T, n_moons) * (t_max - t_min) .+ t_min
    outer_circ_x = cos.(t_outer)
    outer_circ_y = sin.(t_outer) .+ T(1)
    inner_circ_x = 1 .- cos.(t_inner)
    inner_circ_y = 1 .- sin.(t_inner) .- T(1)

    data = [outer_circ_x outer_circ_y; inner_circ_x inner_circ_y]
    z = permutedims(data, (2, 1))
    noise !== nothing && (z .+= T(noise) * randn(rng, T, size(z)))
    return z
end

Let's visualize the dataset

fig = Figure()
ax = CairoMakie.Axis(fig[1, 1]; xlabel="x", ylabel="y")

z = make_moons(Random.default_rng(), Float32, 10_000; noise=0.1)
scatter!(ax, z[1, :], z[2, :]; markersize=2)

fig

---

function load_moons_dataloader(
    args...; batchsize::Int, noise::Union{Nothing,AbstractFloat}=nothing, kwargs...
)
    return DataLoader(
        make_moons(args...; noise); batchsize, shuffle=true, partial=false, kwargs...
    )
end

Bijectors Implementation

abstract type AbstractBijector end

@concrete struct AffineBijector <: AbstractBijector
    shift <: AbstractArray
    log_scale <: AbstractArray
end

function AffineBijector(shift_and_log_scale::AbstractArray{T,N}) where {T,N}
    n = size(shift_and_log_scale, 1) ÷ 2
    idxs = ntuple(Returns(Colon()), N - 1)
    return AffineBijector(
        shift_and_log_scale[1:n, idxs...], shift_and_log_scale[(n + 1):end, idxs...]
    )
end

function forward_and_log_det(bj::AffineBijector, x::AbstractArray)
    y = x .* exp.(bj.log_scale) .+ bj.shift
    return y, bj.log_scale
end

function inverse_and_log_det(bj::AffineBijector, y::AbstractArray)
    x = (y .- bj.shift) ./ exp.(bj.log_scale)
    return x, -bj.log_scale
end

@concrete struct MaskedCoupling <: AbstractBijector
    mask <: AbstractArray
    conditioner
    bijector
end

function apply_mask(bj::MaskedCoupling, x::AbstractArray, fn::F) where {F}
    x_masked = x .* (1 .- bj.mask)
    bijector_params = bj.conditioner(x_masked)
    y, log_det = fn(bijector_params)
    log_det = log_det .* bj.mask
    y = ifelse.(bj.mask, y, x)
    return y, dsum(log_det; dims=Tuple(collect(1:(ndims(x) - 1))))
end

function forward_and_log_det(bj::MaskedCoupling, x::AbstractArray)
    return apply_mask(bj, x, params -> forward_and_log_det(bj.bijector(params), x))
end

function inverse_and_log_det(bj::MaskedCoupling, y::AbstractArray)
    return apply_mask(bj, y, params -> inverse_and_log_det(bj.bijector(params), y))
end

Model Definition

function MLP(in_dims::Int, hidden_dims::Int, out_dims::Int, n_layers::Int; activation=gelu)
    return Chain(
        Dense(in_dims => hidden_dims, activation),
        [Dense(hidden_dims => hidden_dims, activation) for _ in 1:(n_layers - 1)]...,
        Dense(hidden_dims => out_dims),
    )
end

@concrete struct RealNVP <: AbstractLuxContainerLayer{(:conditioners,)}
    conditioners
    dist_dims::Int
    n_transforms::Int
end

const StatefulRealNVP{M} = StatefulLuxLayer{M,<:RealNVP}

function Lux.initialstates(rng::AbstractRNG, l::RealNVP)
    mask_list = Vector{Bool}[
        collect(1:(l.dist_dims)) .% 2 .== i % 2 for i in 1:(l.n_transforms)
    ]
    return (; mask_list, conditioners=Lux.initialstates(rng, l.conditioners))
end

function RealNVP(; n_transforms::Int, dist_dims::Int, hidden_dims::Int, n_layers::Int)
    conditioners = [
        MLP(dist_dims, hidden_dims, 2 * dist_dims, n_layers; activation=gelu) for
        _ in 1:n_transforms
    ]
    conditioners = NamedTuple{ntuple(Base.Fix1(Symbol, :conditioners_), n_transforms)}(
        Tuple(conditioners)
    )
    return RealNVP(conditioners, dist_dims, n_transforms)
end

log_prob(x::AbstractArray{T}) where {T} = -T(0.5 * log(2π)) .- T(0.5) .* abs2.(x)

function log_prob(l::StatefulRealNVP, x::AbstractArray{T}) where {T}
    smodels = [
        StatefulLuxLayer{true}(conditioner, l.ps.conditioners[i], l.st.conditioners[i]) for
        (i, conditioner) in enumerate(l.model.conditioners)
    ]

    lprob = zeros_like(x, size(x, ndims(x)))
    for (mask, conditioner) in Iterators.reverse(zip(l.st.mask_list, smodels))
        bj = MaskedCoupling(mask, conditioner, AffineBijector)
        x, log_det = inverse_and_log_det(bj, x)
        lprob += log_det
    end
    lprob += dsum(log_prob(x); dims=Tuple(collect(1:(ndims(x) - 1))))

    conditioners = NamedTuple{
        ntuple(Base.Fix1(Symbol, :conditioners_), l.model.n_transforms)
    }(
        Tuple([smodel.st for smodel in smodels])
    )
    l.st = merge(l.st, (; conditioners))

    return lprob
end

function sample(
    rng::AbstractRNG,
    ::Type{T},
    d::StatefulRealNVP,
    nsamples::Int,
    nsteps::Int=length(d.model.conditioners),
) where {T}
    @assert 1 ≤ nsteps ≤ length(d.model.conditioners)

    smodels = [
        StatefulLuxLayer{true}(conditioner, d.ps.conditioners[i], d.st.conditioners[i]) for
        (i, conditioner) in enumerate(d.model.conditioners)
    ]

    x = randn(rng, T, d.model.dist_dims, nsamples)
    for (i, (mask, conditioner)) in enumerate(zip(d.st.mask_list, smodels))
        x, _ = forward_and_log_det(MaskedCoupling(mask, conditioner, AffineBijector), x)
        i ≥ nsteps && break
    end
    return x
end

Helper Functions

dsum(x; dims) = dropdims(sum(x; dims); dims)

function loss_function(model, ps, st, x)
    smodel = StatefulLuxLayer{true}(model, ps, st)
    lprob = log_prob(smodel, x)
    return -mean(lprob), smodel.st, (;)
end

Training the Model

function main(;
    maxiters::Int=10_000,
    n_train_samples::Int=100_000,
    batchsize::Int=128,
    n_transforms::Int=6,
    hidden_dims::Int=16,
    n_layers::Int=4,
    lr::Float64=0.0004,
    noise::Float64=0.06,
)
    rng = Random.default_rng()
    Random.seed!(rng, 0)

    dataloader = Iterators.cycle(
        xdev(load_moons_dataloader(rng, Float32, n_train_samples; batchsize, noise))
    )

    model = RealNVP(; n_transforms, dist_dims=2, hidden_dims, n_layers)
    ps, st = xdev(Lux.setup(rng, model))
    opt = Adam(lr)

    train_state = Training.TrainState(model, ps, st, opt)
    @printf "Total Trainable Parameters: %d\n" Lux.parameterlength(ps)

    total_samples = 0
    start_time = time()

    for (iter, x) in enumerate(dataloader)
        total_samples += size(x, ndims(x))
        (_, loss, _, train_state) = Training.single_train_step!(
            AutoEnzyme(), loss_function, x, train_state; return_gradients=Val(false)
        )

        isnan(loss) && error("NaN loss encountered in iter $(iter)!")

        if iter == 1 || iter == maxiters || iter % 1000 == 0
            throughput = total_samples / (time() - start_time)
            @printf "Iter: [%6d/%6d]\tTraining Loss: %.6f\t\
                     Throughput: %.6f samples/s\n" iter maxiters loss throughput
        end

        iter ≥ maxiters && break
    end

    return StatefulLuxLayer{true}(
        model, train_state.parameters, Lux.testmode(train_state.states)
    )
end

trained_model = main()

Visualizing the Results

z_stages = Matrix{Float32}[]
for i in 1:(trained_model.model.n_transforms)
    z = @jit sample(Random.default_rng(), Float32, trained_model, 10_000, i)
    push!(z_stages, Array(z))
end

begin
    fig = Figure(; size=(1200, 800))

    for (idx, z) in enumerate(z_stages)
        i, j = (idx - 1) ÷ 3, (idx - 1) % 3
        ax = Axis(fig[i, j]; title="$(idx) transforms")
        scatter!(ax, z[1, :], z[2, :]; markersize=2)
    end

    fig
end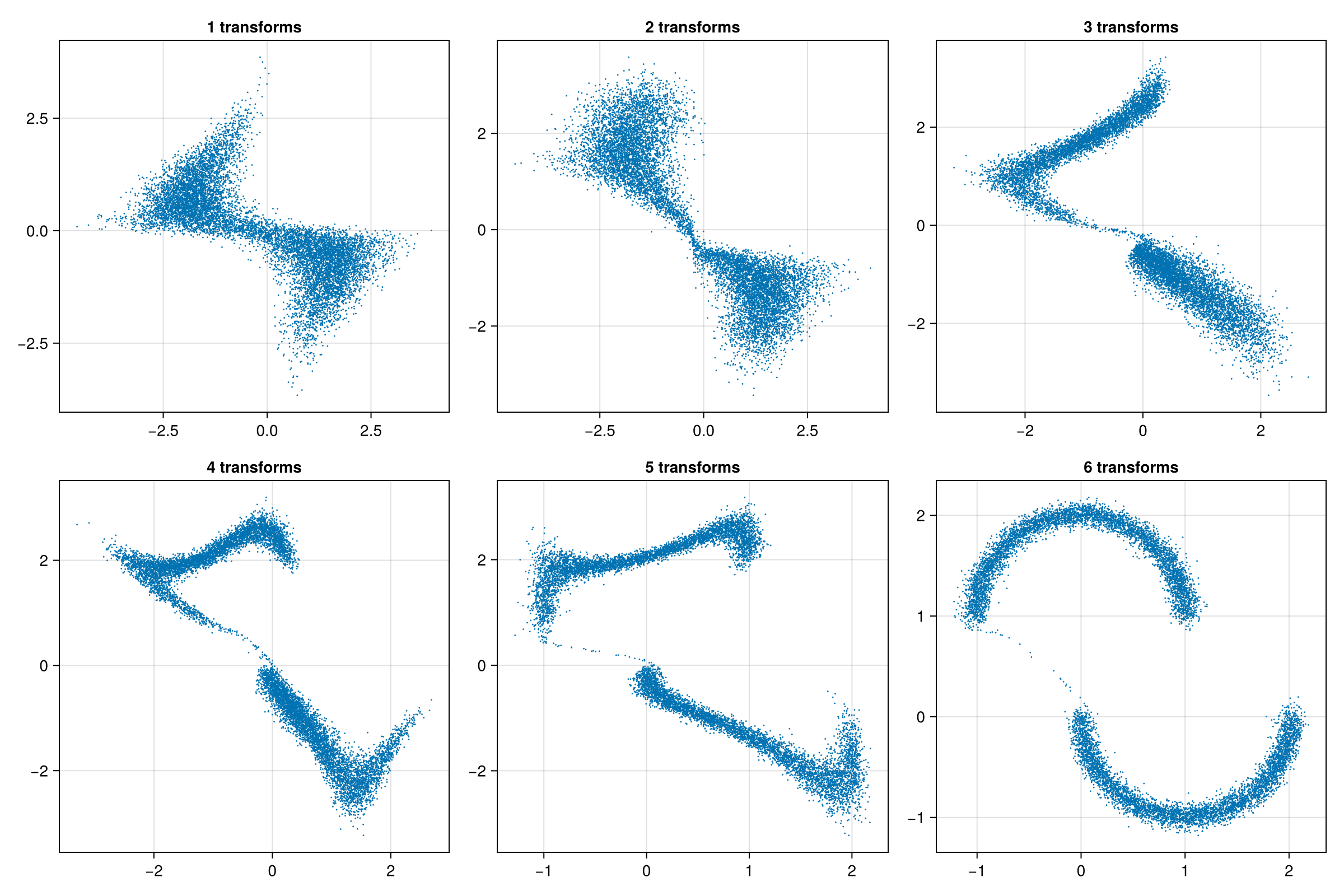

---

This page was generated using Literate.jl.